이전에 o1 나왔을 때 수능수학 풀게 해서 글 올린 적 있었는데
이번에 2025 수능 수학은 왠지 모르겠는데 o1이 잘 못 푸는 문제가 몇 개 있었음
oai 측에서 토큰 이슈 떄문에 성능을 일부러 낮췄을 수도 있고, 아니면 뇌피셜이긴 하지만 평가원이 일부러 부정행위 등 방지하기 위해 인공지능이 잘 못 푸는 문제로 냈을 수도 있음
이번에 새로 나온 Gemini 1114는 어떨까? 하고 수능 문제 똑같이 수식 Latex으로 입력해서 별도의 성능 향상에 도움되는 프롬프트 없이 풀게 해봄
또한 객관식은 선택지를 제거한 형태로 문제를 제공함
본인 서울대 수학과라 풀이과정도 검토 가능하니 검토과정도 같이 올려보겠음
-------------------------------------------------------------------
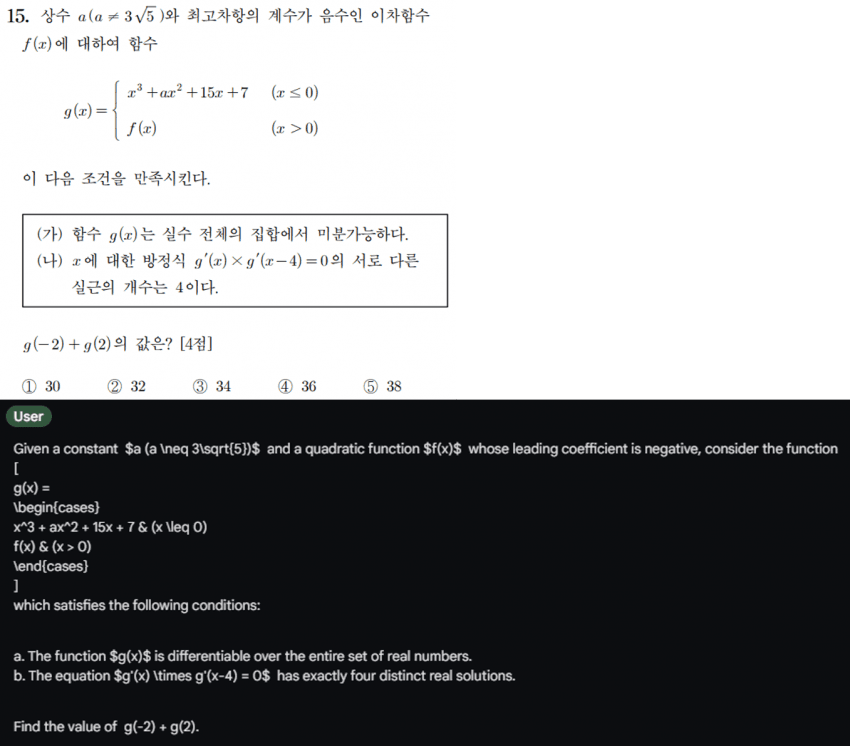
먼저 15번, (나) 조건에서 g'(x)=0 이 되는 곳이 전부 4 간격으로 떨어져 있어야 한다는 걸 추론하면 되는 문제
이걸 떠올리면 x<0 인 부분에서 이차함수 3x^2 + 2ax + 15 의 두 근의 차가 4가 된다는 걸로부터 a값을 쉽게 구할 수 있고, f(x)도 찾을 수 있음
단순히 계산으로 풀 수 있는 문제가 아니기 때문에 단순한 인공지능에겐 어려울 수 있는 문제이고, o1도 풀지 못했었음.

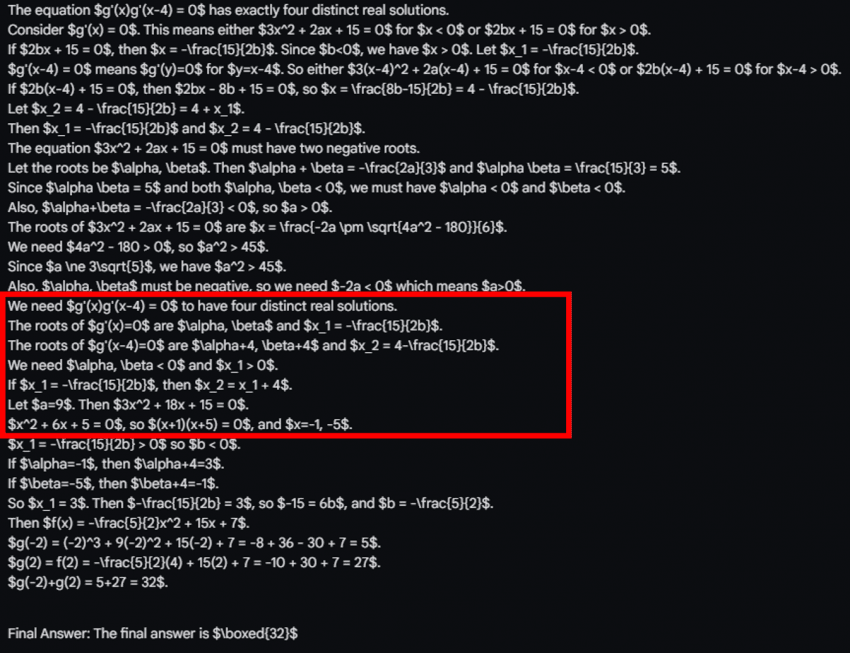
풀이과정이 사실 완전히 엄밀하진 않지만 (x<0인 부분에서 g'(x)의 근이 한 개만 발생하는 경우가 불가능하다는 과정이 생략됨),
어쨌든 (가)(나) 조건을 만족하는 상황을 잘 캐치해냄. 특이한 점은 a=9가 계산과정 없이 바로 나왔다는 건데, 아마 계산과정은 생략해서 보여준듯?
아무튼 찍어서 맞은 게 아니라 변수 값들이랑 f(x)까지 실제 답이랑 똑같이 잘 구해냄.
20번 정답 : 32
Gemini 제출 : 32 (O)
-------------------------------------------------------------------

k값 범위 추론하고, f(f(x)) = 3x 라는 식에서 1/(k^3 * 5^3k) 가 x 자리가 아니라 f(x) 자리에 들어가야 한다는 것만 추론하면
x = 12 대입해서 쉽게 풀 수 있는 문제
근데 비정형화된 문제라서 어려웠다는 사람들이 많고, 실제로 인공지능이 풀기에도 불리한 문제라 o1도 오답을 냈었음


풀이과정에서 불필요한 과정이 좀 많긴 했지만(중간 생략함) k에 관련된 식 세우고, f(x) 식도 제대로 찾아서 대입해서 풀음
20번 정답 : 36
Gemini 제출 : 36 (O)
-------------------------------------------------------------------

21번은 주어진 조건으로부터 f(x)=0의 근이 -1밖에 없어야 한다는 걸 추론한 후 인수분해해서 판별식 쓰면 쉽게 풀 수 있는 문제
이것도 왠지 모르겠는데 o1은 이 간단한 추론을 못 해서 한참 헤맸었음... 처음 나왔을 때 폼이면 금방 발견했을 거라고 생각하긴 함
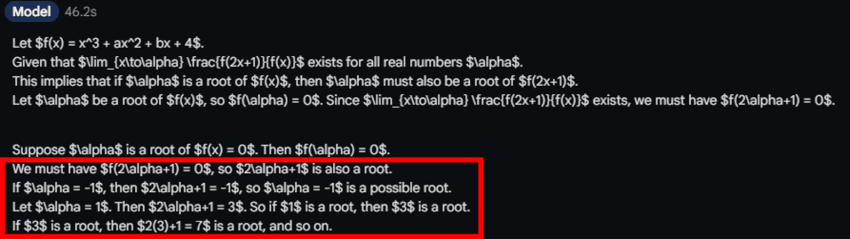

빨간색 박스 친 부분이 핵심. 1이 근이면 3도 근이고, 7도 근이고... 이런 식으로 모순이 발생한다는 걸 인간과 같은 방식으로 추론해냄.
이후 인수분해해서 판별식 써서 범위 구하는 것도 깔끔함
21번 정답 : 16
Gemini 제출 : 16 (O)
-------------------------------------------------------------------

22번은 수열 추론 문제로, 수능 킬러로 출제된 수열 추론 문제는 지금껏 인공지능이 제대로 푼 걸 한 번도 못봤음.
이 문제는 수열 추론 중에서는 비교적 쉬운 편인데, |a_3| 가 될 수 있는 값 먼저 구하고 역추론하면 되기 때문

Gemini는 역시나 a_1 기준으로 경우 나누는 식으로 접근했는데, 안타깝게도 그러면 케이스가 너무 많아져서 다 따지기가 힘듬
실제로 |a_1|이 될 수 있는 값은 6, 7, 8, 9, 10, 24 라서 답이 64가 돼야 하는데, 8, 9, 24만 구해서 틀림
실제로 풀이과정을 보면 케이스가 너무 많아져서 중간에 생략한 케이스들이 있음
22번 정답 : 64
Gemini 제출 : 41 (X)
-------------------------------------------------------------------

미적 28번, f(x)의 식을 구할 수는 없는 형태로 주어졌지만 계산 과정에서 1*f(x) 로 바꾸어 부분적분하는 아이디어로 풀 수 있는 문제


처음엔 g'(1)은 3/2로 잘 구했는데 g(1)은 계산 못했는지 그냥 답을 3/2로 내버림
실제로 g(1)은 계산할 때 앞서 언급한 부분적분 테크닉을 사용해야 되는데 그걸 못 떠올리고, f(x)를 그냥 못 구한다고 판단해버린듯


그래서 힌트 주니까 g(1)도 e/2 - 5/6 로 잘 구해냄
28번 정답 : e/2 + 2/3
Gemini 제출 : 2/3 (X)
(최초 오답, 힌트 받은 후 정답)
-------------------------------------------------------------------

미적 29번, 공비가 -1/2 인거 구해내고 초항도 계산한 후에, 마지막으로 합을 구하고자 하는 수열의 부호의 주기가 4라는 걸 이용해서 계산하는 문제
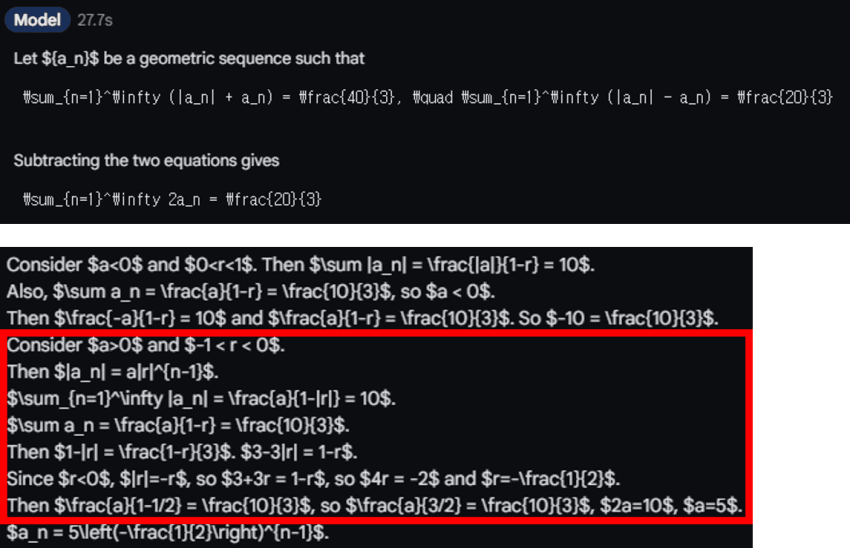
초항/공비 부호에 따라서 케이스 잘 나눴고, 공비가 -1/2 인 거랑 초항이 5인 것까지 제대로 계산해냄.

근데 마지막에 수열의 합 구하는 과정에서 m 대신에 m-1 로 계산했고, 공비도 이상하게 1/2 로 집어넣어서 계산을 틀림
답은 1+3+5+7+9 = 25 가 나와야 하는데 1+2+...+11 = 66 로 구해서 오답.
참고로 이 문제는 o1한테도 물어봤는데 o1도 초항, 공비까지 잘 구해놓고 마지막 부분에서 계산 실수해서 틀리더라...
29번 정답 : 25
Gemini 제출 : 66 (X)
-------------------------------------------------------------------

sinx = x 를 만족하는 x가 0밖에 없다는 거 이용해서 b = -2pi a 구하고,
a = 1, 3/2, 2 나오는데 주기성 따져서 a = 3/2 인 거 구하고,
f(x) 극대점 구하기 위해 f'(x)의 부호 판별하는 과정에서 sinx = -3/2 x - 3pi 를 만족하는 x들 찾아야 하는데 이건 그래프 그려서 구할 수 있는 문제
다 인간한테는 당연한 추론인데 현재 인공지능이 해내기 어려운 것들이기는 함

b = -2pi a 인 것(첫번째 추론) 까지는 해냈는데, (나) 조건에서 핵심을 파악하지 못해서 a = 3/2 를 못 구해냄
a를 못 구했으니 당연히 이후 과정은 나가리
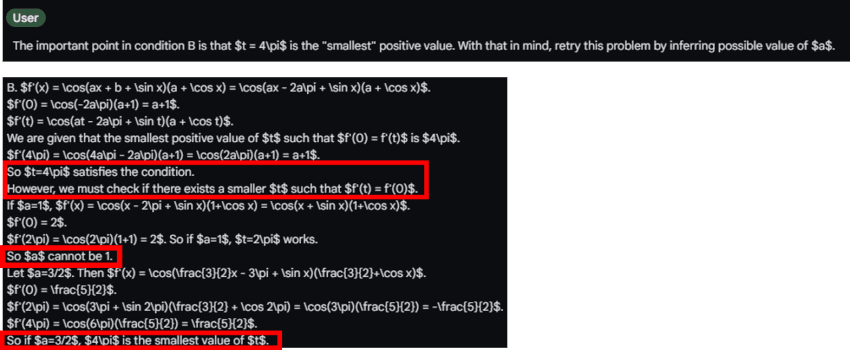
이후 별도로 힌트 주니까 a = 3/2 인거 잘 추론해내긴 했는데, sinx = -3/2 x - 3pi 를 만족하는 x 값 찾는 과정에서 또 막힘
인간이라면 당연히 그래프 그려서 구할 생각을 할 텐데, 아직은 수식적으로 구하려고만 하고 그래프 쪽 추론에는 약한 듯함
(나중에 멀티모달+추론이 되면 나아질 수도?)
30번 정답 : 15pi/2
Gemini 제출 : 5pi (X)
-----------------------------------------------------------------------------------------
전체적으로 준킬러-킬러 문제들만 풀게 해봤는데 킬러 4문제(22, 28, 29, 30) 틀려서 점수는 84점 이하지만,
추론 시간이 지나치게 짧다는 거 감안하면 시간 더 주면 22, 28, 29는 맞출 수 있었을 거라고 생각함 (특히 22, 29는 단순 계산실수)
왠지 모르겠지만 2분 동안 생각하라고 해도 이악물고 30-40초만 생각하더라
그리고 특이한 게 o1이랑 달리 문제 입력하면 생각 시간 같은 거 없이 실시간으로 쓰면서 추론하는데, 이걸 보면 Gemini-1114 자체가 추론이랑 수학 문제 푸는 데에 특화된 건 아닌 것 같긴 함. 특히 풀이과정 읽어보면 시간 제한 때문에 좀만 막히면 바로 제출해버리는 느낌이었음.
아무튼 불과 3개월 전까지만 해도 간단한 계산도 못하던 거 생각하면 장족의 발전이니 곧 수능따위는 씹어먹을 수 있을 것 같고, 이 시리즈는 o1 정식이나 다른 추론 인공지능 나오면 계속 해볼 예정